Lab goals:
- Read a datafile in R
- Print summary statistics
- Conduct correlational analyses
- Examine relationships among variables using scatterplots
Example
- Investigating the effects of sport-related concussion
library(psych)
library(gclus)## Loading required package: clusterlibrary(rgl)Reading in the data
impact <- read.table("Stats1.13.Lab.03.txt", header = T)
describe(impact)## var n mean sd median trimmed mad min max range skew
## subject 1 40 20.50 11.69 20.50 20.50 14.83 1.00 40.00 39.00 0.00
## condition* 2 40 1.50 0.51 1.50 1.50 0.74 1.00 2.00 1.00 0.00
## vermem1 3 40 89.75 6.44 91.00 90.44 6.67 75.00 98.00 23.00 -0.70
## vismem1 4 40 74.88 8.60 75.00 74.97 9.64 59.00 91.00 32.00 -0.11
## vms1 5 40 34.03 3.90 33.50 34.02 3.62 26.29 41.87 15.58 0.08
## rt1 6 40 0.67 0.15 0.65 0.66 0.13 0.42 1.20 0.78 1.14
## ic1 7 40 8.28 2.05 8.50 8.38 2.22 2.00 12.00 10.00 -0.57
## sym1 8 40 0.05 0.22 0.00 0.00 0.00 0.00 1.00 1.00 3.98
## vermem2 9 40 82.00 11.02 85.00 82.97 9.64 59.00 97.00 38.00 -0.65
## vismem2 10 40 71.90 8.42 72.00 72.19 10.38 54.00 86.00 32.00 -0.28
## vms2 11 40 35.83 8.66 35.15 34.98 6.89 20.15 60.77 40.62 0.86
## rt2 12 40 0.67 0.22 0.65 0.65 0.13 0.19 1.30 1.11 0.93
## ic2 13 40 6.75 2.98 7.00 6.81 2.97 1.00 12.00 11.00 -0.16
## sym2 14 40 13.88 15.32 7.00 12.38 10.38 0.00 43.00 43.00 0.44
## kurtosis se
## subject -1.29 1.85
## condition* -2.05 0.08
## vermem1 -0.51 1.02
## vismem1 -0.96 1.36
## vms1 -0.75 0.62
## rt1 2.21 0.02
## ic1 0.36 0.32
## sym1 14.16 0.03
## vermem2 -0.81 1.74
## vismem2 -0.87 1.33
## vms2 0.65 1.37
## rt2 1.29 0.03
## ic2 -1.06 0.47
## sym2 -1.47 2.42describeBy(impact, impact$condition)## group: concussed
## var n mean sd median trimmed mad min max range skew
## subject 1 20 30.50 5.92 30.50 30.50 7.41 21.00 40.00 19.00 0.00
## condition* 2 20 1.00 0.00 1.00 1.00 0.00 1.00 1.00 0.00 NaN
## vermem1 3 20 89.65 7.17 92.50 90.56 5.93 75.00 97.00 22.00 -0.79
## vismem1 4 20 74.75 8.03 74.00 74.25 8.15 63.00 91.00 28.00 0.45
## vms1 5 20 33.20 3.62 33.09 33.27 3.32 26.29 39.18 12.89 -0.13
## rt1 6 20 0.66 0.17 0.63 0.64 0.13 0.42 1.20 0.78 1.38
## ic1 7 20 8.55 1.64 9.00 8.62 1.48 5.00 11.00 6.00 -0.39
## sym1 8 20 0.05 0.22 0.00 0.00 0.00 0.00 1.00 1.00 3.82
## vermem2 9 20 74.05 9.86 74.00 73.88 11.86 59.00 91.00 32.00 0.07
## vismem2 10 20 69.20 8.38 69.50 69.62 10.38 54.00 80.00 26.00 -0.27
## vms2 11 20 38.27 10.01 35.15 37.32 7.73 25.70 60.77 35.07 0.77
## rt2 12 20 0.78 0.23 0.70 0.74 0.11 0.51 1.30 0.79 1.09
## ic2 13 20 5.00 2.53 5.00 4.88 2.97 1.00 11.00 10.00 0.39
## sym2 14 20 27.65 9.07 27.00 27.75 11.12 13.00 43.00 30.00 -0.11
## kurtosis se
## subject -1.38 1.32
## condition* NaN 0.00
## vermem1 -0.70 1.60
## vismem1 -0.72 1.80
## vms1 -0.78 0.81
## rt1 2.41 0.04
## ic1 -0.81 0.37
## sym1 13.29 0.05
## vermem2 -1.24 2.21
## vismem2 -1.26 1.87
## vms2 -0.57 2.24
## rt2 -0.10 0.05
## ic2 -0.28 0.57
## sym2 -1.25 2.03
## --------------------------------------------------------
## group: control
## var n mean sd median trimmed mad min max range skew
## subject 1 20 10.50 5.92 10.50 10.50 7.41 1.00 20.00 19.00 0.00
## condition* 2 20 2.00 0.00 2.00 2.00 0.00 2.00 2.00 0.00 NaN
## vermem1 3 20 89.85 5.82 90.00 90.31 7.41 78.00 98.00 20.00 -0.41
## vismem1 4 20 75.00 9.34 77.00 75.50 9.64 59.00 88.00 29.00 -0.46
## vms1 5 20 34.86 4.09 34.39 34.85 4.92 27.36 41.87 14.51 0.09
## rt1 6 20 0.67 0.13 0.66 0.67 0.13 0.42 1.00 0.58 0.47
## ic1 7 20 8.00 2.41 7.50 8.12 2.22 2.00 12.00 10.00 -0.41
## sym1 8 20 0.05 0.22 0.00 0.00 0.00 0.00 1.00 1.00 3.82
## vermem2 9 20 89.95 4.36 90.50 90.06 5.19 81.00 97.00 16.00 -0.25
## vismem2 10 20 74.60 7.76 74.50 75.00 8.15 60.00 86.00 26.00 -0.23
## vms2 11 20 33.40 6.44 34.54 33.52 6.30 20.15 44.28 24.13 -0.25
## rt2 12 20 0.57 0.16 0.56 0.57 0.13 0.19 0.90 0.71 -0.16
## ic2 13 20 8.50 2.31 9.00 8.69 1.48 3.00 12.00 9.00 -0.73
## sym2 14 20 0.10 0.31 0.00 0.00 0.00 0.00 1.00 1.00 2.47
## kurtosis se
## subject -1.38 1.32
## condition* NaN 0.00
## vermem1 -0.87 1.30
## vismem1 -1.27 2.09
## vms1 -1.19 0.91
## rt1 -0.02 0.03
## ic1 -0.17 0.54
## sym1 13.29 0.05
## vermem2 -1.02 0.97
## vismem2 -1.11 1.73
## vms2 -0.77 1.44
## rt2 0.06 0.04
## ic2 -0.32 0.52
## sym2 4.32 0.07Correlation analysis of baseline measures
cor(impact[3:8]) # columns 3 to 8 contains the 6 baseline measures## vermem1 vismem1 vms1 rt1 ic1 sym1
## vermem1 1.00000 0.37512 -0.040567 0.1467 0.131471 0.13521
## vismem1 0.37512 1.00000 -0.233391 0.1361 0.237559 0.01689
## vms1 -0.04057 -0.23339 1.000000 -0.1320 0.005221 -0.05190
## rt1 0.14673 0.13615 -0.131955 1.0000 0.121334 -0.03390
## ic1 0.13147 0.23756 0.005221 0.1213 1.000000 0.08215
## sym1 0.13521 0.01689 -0.051903 -0.0339 0.082149 1.00000Round to 2 decimal places.
round(cor(impact[3:8]), 2)## vermem1 vismem1 vms1 rt1 ic1 sym1
## vermem1 1.00 0.38 -0.04 0.15 0.13 0.14
## vismem1 0.38 1.00 -0.23 0.14 0.24 0.02
## vms1 -0.04 -0.23 1.00 -0.13 0.01 -0.05
## rt1 0.15 0.14 -0.13 1.00 0.12 -0.03
## ic1 0.13 0.24 0.01 0.12 1.00 0.08
## sym1 0.14 0.02 -0.05 -0.03 0.08 1.00Create two subsets, control and concussedd
control <- subset(impact, impact[, 2] == "control")
concussed <- subset(impact, impact[, 2] == "concussed")
control## subject condition vermem1 vismem1 vms1 rt1 ic1 sym1 vermem2 vismem2
## 1 1 control 95 88 35.29 0.42 11 0 97 86
## 2 2 control 90 82 31.47 0.63 7 0 86 80
## 3 3 control 87 77 30.87 0.56 8 0 90 79
## 4 4 control 84 72 41.87 0.66 7 0 85 70
## 5 5 control 92 77 33.28 0.56 7 1 87 77
## 6 6 control 89 79 40.73 0.81 6 0 91 85
## 7 7 control 78 63 38.09 0.66 6 0 90 60
## 8 8 control 97 82 31.65 0.79 10 0 94 72
## 9 9 control 93 85 39.59 0.68 7 0 91 83
## 10 10 control 90 66 30.53 0.60 10 0 93 68
## 11 11 control 89 76 33.65 0.74 7 0 92 72
## 12 12 control 97 79 37.51 0.51 7 0 89 79
## 13 13 control 79 60 40.39 0.82 12 0 84 67
## 14 14 control 86 59 32.88 0.59 2 0 81 71
## 15 15 control 85 60 33.39 0.82 9 0 85 61
## 16 16 control 85 76 35.13 0.63 10 0 87 72
## 17 17 control 98 85 38.51 0.73 10 0 96 78
## 18 18 control 95 83 29.64 0.57 8 0 93 85
## 19 19 control 96 67 35.32 0.65 5 0 95 67
## 20 20 control 92 84 27.36 1.00 11 0 93 80
## vms2 rt2 ic2 sym2
## 1 35.61 0.65 10 0
## 2 37.01 0.49 7 0
## 3 20.15 0.75 9 0
## 4 33.26 0.19 8 0
## 5 28.34 0.59 8 1
## 6 33.47 0.48 5 0
## 7 44.28 0.77 6 0
## 8 36.14 0.90 10 0
## 9 37.42 0.65 8 0
## 10 25.19 0.59 11 0
## 11 23.63 0.55 9 0
## 12 26.32 0.56 9 1
## 13 43.70 0.57 10 0
## 14 32.40 0.69 3 0
## 15 39.32 0.73 10 0
## 16 35.62 0.48 12 0
## 17 39.95 0.43 10 0
## 18 35.62 0.37 9 0
## 19 30.21 0.47 5 0
## 20 30.37 0.50 11 0concussed## subject condition vermem1 vismem1 vms1 rt1 ic1 sym1 vermem2 vismem2
## 21 21 concussed 79 81 27.19 0.57 7 0 63 75
## 22 22 concussed 85 85 32.66 0.71 9 0 79 79
## 23 23 concussed 97 91 26.29 0.82 9 0 91 80
## 24 24 concussed 89 74 28.92 0.61 9 0 85 72
## 25 25 concussed 75 63 32.77 0.72 8 0 74 56
## 26 26 concussed 75 68 32.92 0.50 9 0 72 66
## 27 27 concussed 84 78 34.26 0.54 6 0 80 74
## 28 28 concussed 93 74 36.08 0.65 10 0 59 69
## 29 29 concussed 88 80 31.63 0.66 9 0 75 79
## 30 30 concussed 97 73 28.89 0.71 7 0 90 73
## 31 31 concussed 93 74 35.81 0.55 9 0 66 69
## 32 32 concussed 96 70 33.61 0.79 7 0 85 61
## 33 33 concussed 84 81 34.46 0.48 7 0 72 79
## 34 34 concussed 89 72 39.18 0.55 10 0 82 66
## 35 35 concussed 95 90 33.14 1.20 10 0 80 80
## 36 36 concussed 95 74 33.03 0.73 11 1 59 70
## 37 37 concussed 97 70 39.01 0.60 10 0 74 62
## 38 38 concussed 95 63 35.06 0.84 5 0 62 54
## 39 39 concussed 92 65 30.58 0.60 8 0 67 57
## 40 40 concussed 95 69 38.45 0.42 11 0 66 63
## vms2 rt2 ic2 sym2
## 21 29.23 0.61 3 26
## 22 44.45 0.65 6 34
## 23 26.12 1.12 5 27
## 24 27.98 0.65 5 22
## 25 60.77 0.71 1 26
## 26 31.91 0.79 9 35
## 27 49.62 0.64 7 43
## 28 35.68 0.70 11 31
## 29 55.67 0.68 6 39
## 30 25.70 0.73 3 25
## 31 35.21 0.58 4 31
## 32 33.01 0.97 3 38
## 33 37.46 0.56 1 14
## 34 53.20 0.51 7 16
## 35 33.20 1.30 7 33
## 36 34.59 0.70 4 13
## 37 39.66 0.74 5 27
## 38 35.09 1.24 2 15
## 39 32.30 0.65 6 19
## 40 44.49 0.98 5 39Correlation analysis of the control group, all measures. This is test/retest, so we can test different measures for reliability.
round(cor(control[3:14]), 2)## vermem1 vismem1 vms1 rt1 ic1 sym1 vermem2 vismem2 vms2
## vermem1 1.00 0.69 -0.27 -0.19 0.07 0.09 0.67 0.59 -0.29
## vismem1 0.69 1.00 -0.13 -0.11 0.29 0.05 0.60 0.85 -0.14
## vms1 -0.27 -0.13 1.00 -0.02 -0.13 -0.09 -0.17 -0.10 0.41
## rt1 -0.19 -0.11 -0.02 1.00 0.27 -0.20 -0.03 -0.23 0.26
## ic1 0.07 0.29 -0.13 0.27 1.00 -0.10 0.34 0.08 0.20
## sym1 0.09 0.05 -0.09 -0.20 -0.10 1.00 -0.16 0.07 -0.18
## vermem2 0.67 0.60 -0.17 -0.03 0.34 -0.16 1.00 0.37 -0.14
## vismem2 0.59 0.85 -0.10 -0.23 0.08 0.07 0.37 1.00 -0.23
## vms2 -0.29 -0.14 0.41 0.26 0.20 -0.18 -0.14 -0.23 1.00
## rt2 -0.08 -0.18 -0.26 0.00 0.02 0.03 0.02 -0.24 0.04
## ic2 0.13 0.31 -0.25 0.15 0.90 -0.05 0.28 0.05 -0.03
## sym2 0.27 0.11 0.04 -0.35 -0.14 0.69 -0.15 0.15 -0.32
## rt2 ic2 sym2
## vermem1 -0.08 0.13 0.27
## vismem1 -0.18 0.31 0.11
## vms1 -0.26 -0.25 0.04
## rt1 0.00 0.15 -0.35
## ic1 0.02 0.90 -0.14
## sym1 0.03 -0.05 0.69
## vermem2 0.02 0.28 -0.15
## vismem2 -0.24 0.05 0.15
## vms2 0.04 -0.03 -0.32
## rt2 1.00 -0.01 0.01
## ic2 -0.01 1.00 0.00
## sym2 0.01 0.00 1.00Let’s look at the concussed athletes. We can’t treat this data as test-retest, as there has been the concussion between the two measurements.
round(cor(concussed[3:14]), 2)## vermem1 vismem1 vms1 rt1 ic1 sym1 vermem2 vismem2 vms2
## vermem1 1.00 0.09 0.16 0.36 0.22 0.18 0.11 -0.04 -0.39
## vismem1 0.09 1.00 -0.38 0.36 0.16 -0.02 0.36 0.93 -0.19
## vms1 0.16 -0.38 1.00 -0.26 0.31 -0.01 -0.33 -0.40 0.48
## rt1 0.36 0.36 -0.26 1.00 -0.03 0.09 0.25 0.16 -0.20
## ic1 0.22 0.16 0.31 -0.03 1.00 0.35 -0.12 0.15 0.10
## sym1 0.18 -0.02 -0.01 0.09 0.35 1.00 -0.36 0.02 -0.09
## vermem2 0.11 0.36 -0.33 0.25 -0.12 -0.36 1.00 0.35 -0.06
## vismem2 -0.04 0.93 -0.40 0.16 0.15 0.02 0.35 1.00 -0.16
## vms2 -0.39 -0.19 0.48 -0.20 0.10 -0.09 -0.06 -0.16 1.00
## rt2 0.44 0.14 -0.07 0.71 -0.06 -0.08 0.12 -0.10 -0.29
## ic2 0.02 0.17 0.19 -0.04 0.47 -0.09 -0.05 0.18 0.00
## sym2 -0.11 0.21 0.06 -0.02 0.07 -0.38 0.22 0.21 0.23
## rt2 ic2 sym2
## vermem1 0.44 0.02 -0.11
## vismem1 0.14 0.17 0.21
## vms1 -0.07 0.19 0.06
## rt1 0.71 -0.04 -0.02
## ic1 -0.06 0.47 0.07
## sym1 -0.08 -0.09 -0.38
## vermem2 0.12 -0.05 0.22
## vismem2 -0.10 0.18 0.21
## vms2 -0.29 0.00 0.23
## rt2 1.00 -0.04 0.15
## ic2 -0.04 1.00 0.40
## sym2 0.15 0.40 1.00Does baseline impulse control predict memory impairment after a concussion?
concussed$verbal.impair <- (concussed$vermem1 - concussed$vermem2)
concussed$visual.impair <- (concussed$vismem1 - concussed$vismem2)
concussed$memory.impair <- (concussed$verbal.impair + concussed$visual.impair)/2
cor(concussed$memory.impair, concussed$ic1)## [1] 0.2294Scatterplots
Scatterplot functions are available in many packages and offer an array of advanced features. For the sake of time, I will demonstrate just a few examples here.
Standard scatterplot
par(mfrow = c(1, 1))
plot(impact$vermem1 ~ impact$vismem1)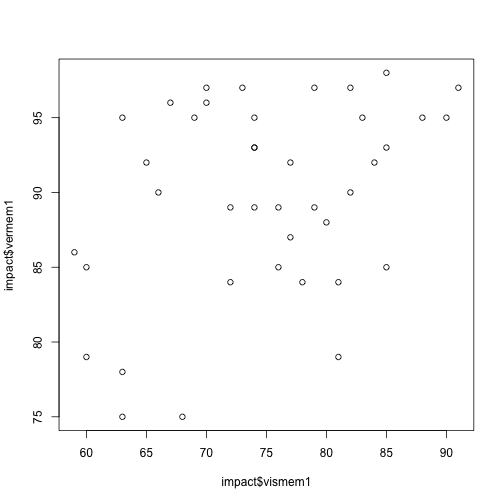
Standard scatterplot with regression line. Positive slope means there is a positive correlation.
par(mfrow = c(1, 1))
plot(impact$vermem1 ~ impact$vismem1)
abline(lm(impact$vermem1 ~ impact$vismem1), col = "green")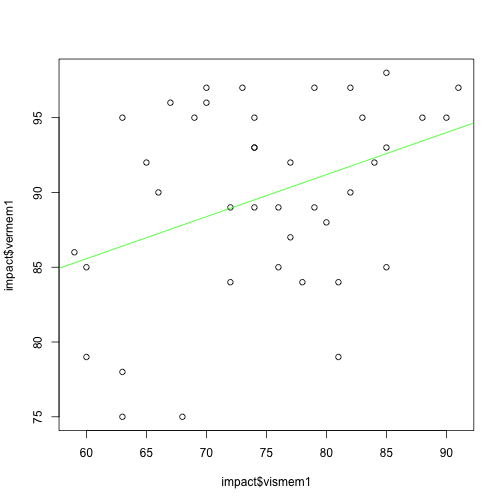
Scatterplot matrix, in order to plot multiple correlations at once
pairs(~impact$vermem1 + impact$vismem1 + impact$vms1 + impact$rt1 + impact$sym1,
cex.labels = 1.2)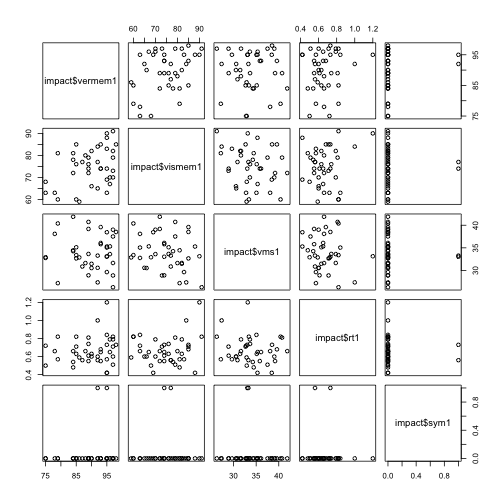
Colored scatterplot matrix, ordered by magnitude of r
base <- impact[3:8]
base.r <- abs(cor(base))
base.color <- dmat.color(base.r)
base.order <- order.single(base.r)
cpairs(base, base.order, panel.colors = base.color, gap = 0.5, main = "Variables Ordered and Colored by Correlation")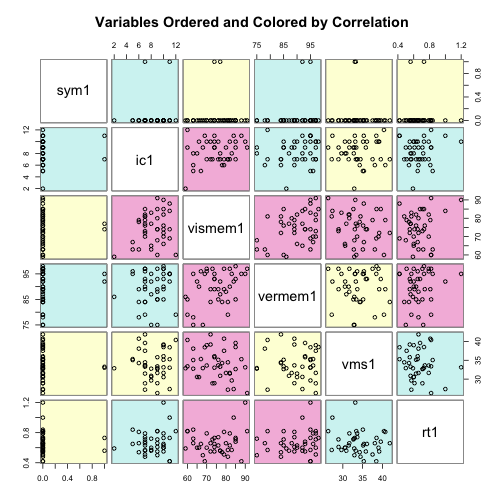
Scatterplots in 3D
plot3d(impact$vismem1, impact$sym1, impact$vermem1)